Chapter 3 – Division (C and D Scale)
3.1 Subtracting with Uniform Scales
Fig. 3.1 shows how we can subtract numbers using a pair of uniform scales (e.g. two ordinary rulers).

Fig 3-1
To Calculate 6 – 2:
- Find 6 on the lower scale.
- Place the 2 of the upper scale over 6.
- the left index (i.e. the 0) of the upper scale indicates the answer as 4 on the lower scale.
3.2 Simple Division
When we subtract numbers on the C and D scales we have division.

Fig 3-2
This is because the lengths we are subtracting are the logarithms of the numbers.
Example 1: 6 ÷ 2 = 3 (Fig. 3-2)
- Set the hair line over 6 on the D scale.
- Place the 2 of the C scale under the hair line.
- Below the left index of the C scale read off the answer as 3 on the D scale.
Note: The hair line on the cursor may be used for division in the following ways.
- To mark the numerator (i.e. number we are dividing into) on the D scale if it does not fall exactly on a graduation, so that the denominator (i.e. number we are dividing by) on the C scale can be set above it.
- Then to set over the index on the C scale so that the answer can be located on easily on the D scale.
Important Points.
- When we set up division on the C and D scale it appears seemingly upside down. To calculate 6 ÷ 2 (i.e.
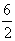 ), we find 6 on the (lower) D scale and 2 is placed above it on the (upper) C scale, thus appearing on the Slide Rule as
), we find 6 on the (lower) D scale and 2 is placed above it on the (upper) C scale, thus appearing on the Slide Rule as  .
.
- For division the answer is always indicated on the D scale by the index of the C scale. If the left index of the C scale runs off the end of the D scale, you will notice that the right index will come onto the D scale. Whichever index comes onto the scale, we can use that index to find the answer.
Example 2: 56 ÷ 7 = 8
- Set the hair line over 56 on the D scale.
- Place the 7 of the C scale under the hair line.
- Below the right index of the C scale read off the answer as 8 on the D scale.
Exercise 3(a)
 =
= =
= =
=- 675 ÷ 326 =
- 196 ÷ 14 =
- 6.6 ÷ 14.2 =
3.3 Locating the Decimal Point
The best method is to make a quick estimate of the answer. This can be accomplished by several different approaches.
Example 1:
194 ÷ 4.15 = ‘467’
(i.e. approx. 200 ÷ 4 = 50)
therefore the answer is 46.7
Standard form (or scientific notation) may be used when very large or vary small numbers are involved.
Example 2:
56000 ÷ 750 = ‘746’
(i.e. approx. (6 x 104) ÷ (8 x 102) = .75 x 102
Good general methods are:
(a) or large numbers divide both numbers by 10, 100, or 1000 etc. (whichever is applicable). That is, cancel corresponding zeros in both numerator and denominator (i.e. top and bottom).
Example 3:
 = ‘145’
= ‘145’
(i.e.  =
= ˜16)
˜16)
therefore the answer is 14.5
(b) For small numbers multiply both by 10, 100, 1000 etc., by moving the decimal point a certain number of places to the right as follows.
Example 4:
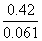 = ‘688’
= ‘688’
(i.e. approx. 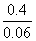 =
=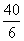 ≈ 7
≈ 7
therefore the answer is 6.88
Exercise 3(b)
Locate the decimal point for the following:
 = ‘878’
= ‘878’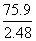 = ‘306’
= ‘306’
 = ‘362’
= ‘362’ = ‘756’
= ‘756’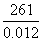 = ‘2175’
= ‘2175’- 9.42 ÷ 216 = ‘436’
- 0.024 ÷ 0.08 = ‘300’
- 520 ÷ 0.45 = ‘1155’
- 0.084 ÷ 0.0025 = ‘336’
- 43500 ÷ 13.6 = ‘32
Note:
- When we divide by a number less than 1, the answer is always larger than the number we are dividing into.
- Unlike multiplication, with division we never run off the end of the D scale for the answer. Either the left or right index of the C scale will always be on the D scale.
3.4 Continuous Division
When dividing a number by 2 or more numbers, after each division, hold the answer on the D scale with the hair line and repeat the division process as many times as necessary. (For combined multiplication and division see Unit 4).
Exercise 3(c)
Miscellaneous Division.
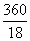 =
=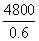 =
= =
= =
=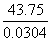 =
=- 3025 ÷ 55 =
- 1925 ÷ 17.5 =
- π χ
2 =
- π χ
6 =
- 93 ÷ 9600 =
 =
= =
= =
= =
= =
=- 0.00593 ÷ 2.66 =
- 0.00207 ÷ 0.000523 =
- 36400 ÷ 26 =
- 20.25 ÷ 0.00045 =
- 0.001035 ÷ 111 =



![]() = ‘145’
= ‘145’![]() =
=![]() ˜16)
˜16)![]() = ‘688’
= ‘688’![]() =
=![]() ≈ 7
≈ 7